Objectif
- Déterminer la contrainte normale.
- Déterminer la contrainte tangentielle.
- Vérifier la condition de résistance.
1. Hypothèses :
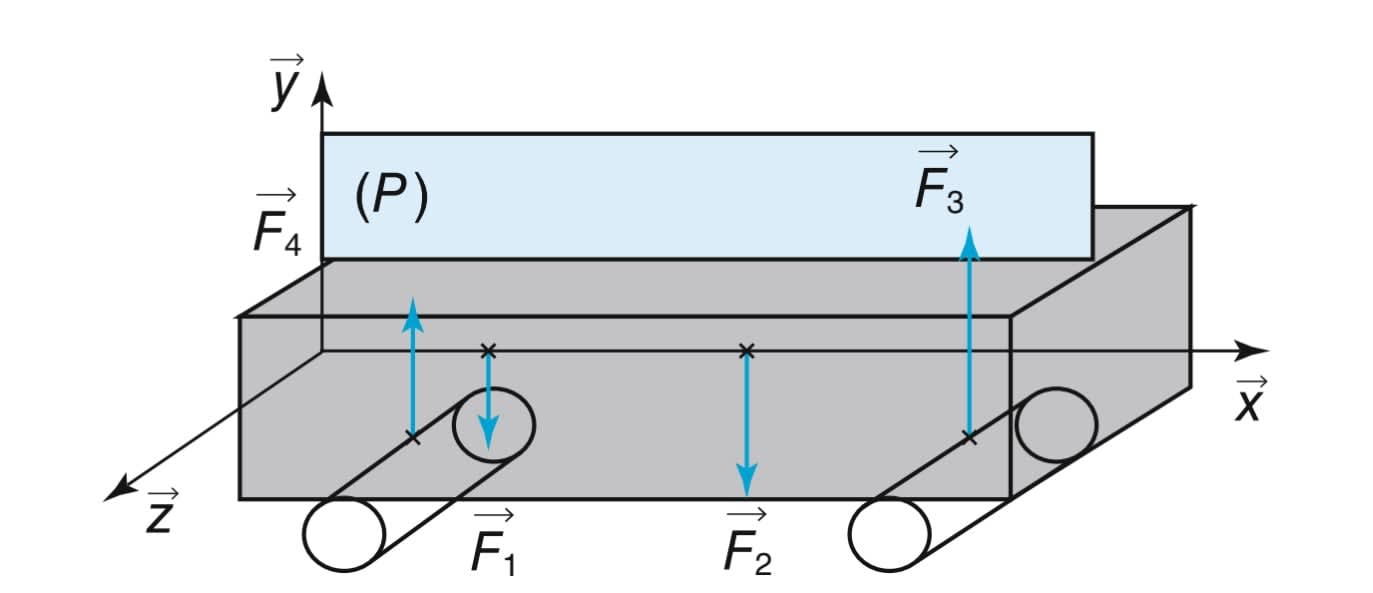
Le solide est une poutre rectiligne de section constante. Le matériau du solide est homogène et isotrope. Les charges sont dans le plan de symétrie de la poutre et perpendiculaire à la ligne moyenne.
2. Définition
Une poutre est soumise à la flexion si le torseur de cohésion dans la section droite est égal à :
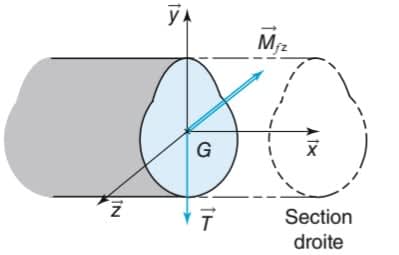
3. Contrainte normale
$\sigma_{\mathrm M}=\dfrac{\mathrm M_{fz}}{\mathrm I_{\mathrm Gz}} \times y$
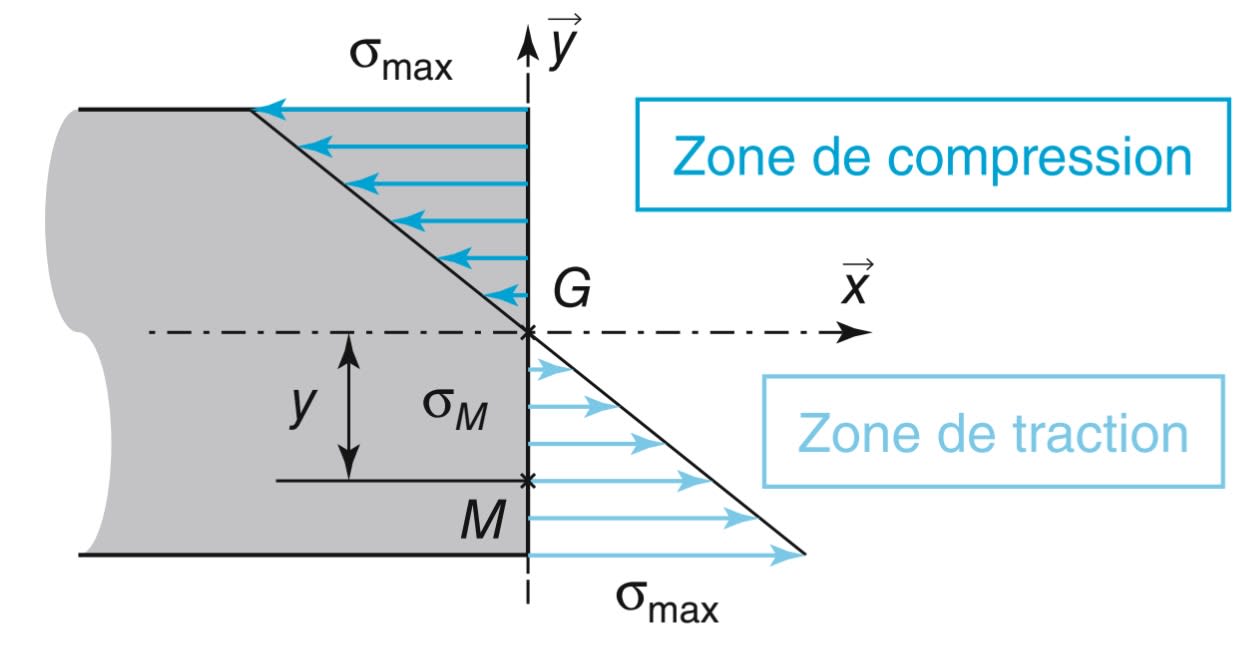
- $\rm \sigma_M$ : contrainte normale en $\rm M$ du à la flexion en $\rm MPa$,
- $\mathrm M_{fz}$ : moment de flexion d’axe $\vec{z}$ en $\rm N.m$,
- $\mathrm I_{\mathrm Gz}$ : Moment quadratique de la section par rapport à $(\mathrm G, \vec{z})$ en $\rm mm^4$,
- $y$ : distance $\rm GM$. On appelle « fibre neutre », le lieu où la contrainte normale est nulle.
4. Contrainte maximale :
La contrainte est maximale pour une distance $\rm GM$ la plus éloignée.
$\sigma_{max}=\dfrac{\mathrm M_{fz}}{\mathrm I_{\mathrm Gz}} \times y_{\rm max}$
On définit le module de flexion :
$\dfrac{\mathrm I_{\mathrm Gz}}{y_{\rm max}}$ ou $\dfrac{\mathrm I_{\mathrm Gz}}{\nu}$
5. Déformation en flexion :
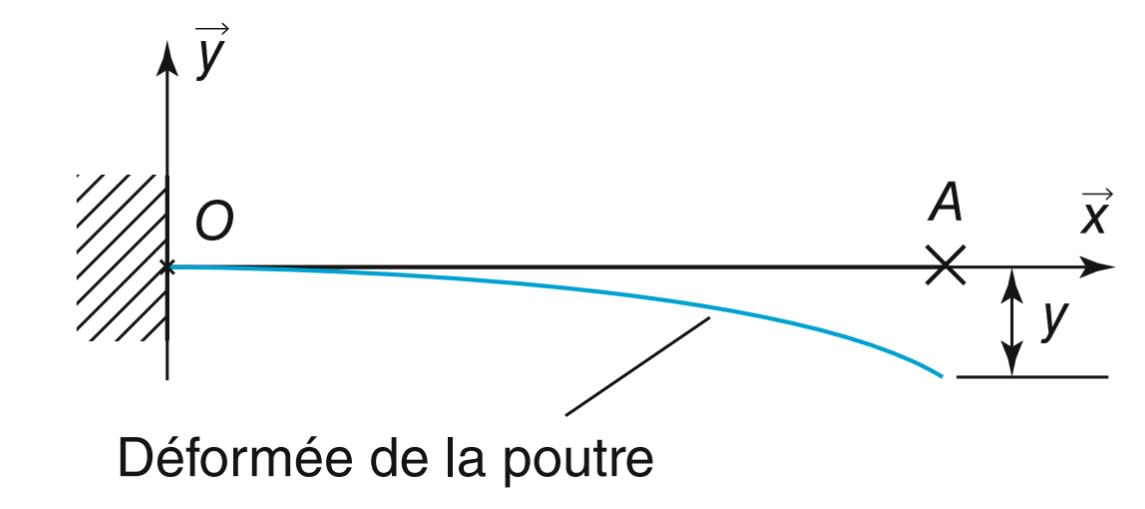
La déformée est définie par :
$y''=\dfrac{\mathrm M_{fz}}{\rm E \times I_{G\mathcal z}}$
Remarque : $y"$ n’est pas la distance $\rm GM$ définie dans la contrainte normale ; c’est la dérivée seconde de la déformée $y = f(x)$.
