Le travail, noté WAB(→F) d'une force constante →F, sur un déplacement AB de son point d'application, est le produit scalaire de la force →F par le déplacement →AB.
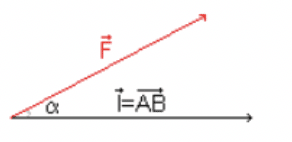
On écrit ainsi : WAB(→F)=→F⋅→AB ou WAB(→F)=F⋅AB⋅cosα
{WAB(→F):Travail de la force →F en Joules (J)→AB:vecteur déplacement du point d'application de la force.AB en mètres (m)α:angle existant entre les vecteurs →F et →AB, en ° (degré) ou enrad (radian)

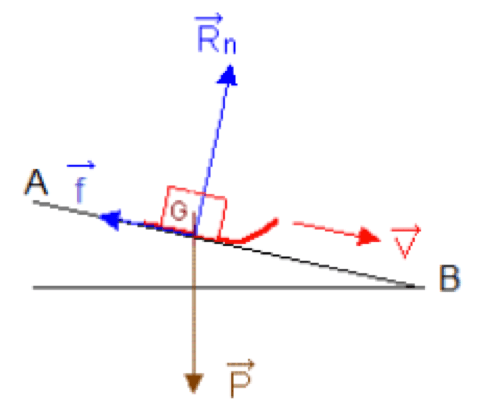
WAB(→P)=→P⋅→AB=m→g⋅→AB
Travail du poids :
WAB(→P)=→P⋅→AB=m→g⋅→AB =mg⋅AB⋅cos(α).
Or dans le triangle OAB représenté ci-dessous :

cos(α)=AOAB⇒AB⋅cos(α)=AO =zA−zo
cos(α)=AOAB⇒AB⋅cos(α) =zA−zB
cos(α)=AOAB⇒WAB(→P)=mg⋅AB ⋅cos(α)=mg(zA−zB)
Bilan : le travail du poids est défini par la relation suivantes :
WAB(→P)=mg(zA−zB)
Il ne dépend que de la variation d'altitude zA−zB (en mètres).