Mouvement de rotation

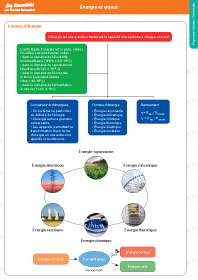
Un système est en rotation si tous les points du système ont pour trajectoire un cercle ayant le même centre.

Tours	1/4 tour	1/2 tour	3/4 tour	1 tour
Degrés	90	180	270	360
Rad	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$2\pi$

Vitesse angulaire : $\rm \omega = \dfrac{\Theta}{\Delta t}$ avec $\Theta$ angle balayé, $\rm\Delta t$ durée du balayage.

	$\color{cornflowerblue}{\omega}$	$\color{cornflowerblue}{\Theta}$	$\color{cornflowerblue}{\bf \Delta t}$
Unités légales	$\color{black}{\rm rad.s^{-1}}$	rad	s
Autre unité usuelle	$\color{black}{\rm tour.min^{-1}}$	tour	min

Vitesse d’un point d’un système en rotation : 

$v=r\omega$ avec $r$ distance entre le point et l’axe de rotation $\Delta$ du système, $\omega$ vitesse angulaire en $\rm rad.s^{-1}$, $v$ vitesse du point considéré en $\rm m.s^{-1}$.

On appelle « bras de levier » $a$ d’une force $\rm \overrightarrow{F}$ par rapport à un axe de rotation $\Delta$ la distance entre la ligne de rotation $\rm \overrightarrow{F}$ et l’axe de rotation.

C’est la longueur du segment qui lie l’axe $\Delta$ à la ligne d’action de la force, le segment étant perpendiculaire à cette ligne d’action.

Unité SI :

Comme le bras de levier est une distance, son unité SI est le mètre (m).

On appelle moment d’une force $\rm \overrightarrow{F}$ par rapport à un axe de rotation $\Delta$ le produit de la norme $\rm F$ de la force et de son bras de levier $a$. Symbole : $\rm M_{\Delta}(\overrightarrow{F})$.

$\rm M_{\Delta}(\overrightarrow{F}) = \pm F\cdot \mathcal a$

Unité SI :

Comme l’unité SI de la norme d’une force est le Newton, celle du bras de levier étant le mètre, l’unité SI du moment d’une force est le « Newton mètre » $\rm(N\cdot m$ ou $\rm Nm)$.

Deux forces s'appliquant sur un système en rotation constituent un couple de force si :

• Elles ont la même direction.
• Elles sont de sens opposé.
• Elles ont la même valeur.