Principe fondamental de la dynamique

Le vecteur-accelération $\vec a (t)$caractérise la variation du vecteur-vitesse en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.

Le vecteur-accélération au point $\mathrm M_i$ s'écrit donc :

$\boxed{\overrightarrow{a(t)} = \frac{\mathrm d\vec v}{\mathrm dt} = \frac{\rm d^2\overrightarrow{OM}}{\mathrm dt^2}} \left\{\begin{array}{ll}t \text{ en s}\\ v \text{ en } \rm m.s^{1}\\ a \text{ en } \rm m.s^{-1}\end{array}\right.$

$\vec a(t) = a_x(t) \vec i + a_y (t) \vec j + a_z(t)\vec k$ avec $\vec a \left|\begin{array}{lll}a_x = \dfrac{\mathrm dv_x}{\mathrm dt} = \dfrac{\mathrm d^2x}{\mathrm dt^2}\\a_y = \dfrac{\mathrm dv_y}{\mathrm dt} = \dfrac{\mathrm d^2y}{\mathrm dt^2}\\a_z = \dfrac{\mathrm dv_z}{\mathrm dt} = \dfrac{\mathrm d^2z}{\mathrm dt^2}\end{array}\right.$

Les caractéristiques du vecteur-accélération sont les suivantes :

$\vec a(t)\left\{\begin{array}{lll}\scriptstyle \text{direction : celle du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{sens : celui du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{valeur (norme) : } a = \frac{\Delta v}{\Delta t} = \|\vec a\| = \sqrt{a_a^2+a_y^2+a_z^2}\end{array}\right.$

Principe fondamental de la dynamique :

$\displaystyle \sum \overrightarrow{\mathrm F} = m\vec a$

Chute libre :

Un solide est en chute libre lorsqu’il n’est soumis qu’à l’action de son poids.

Le système étudié est un solide de masse $m$ et de centre d'inertie $\rm G$.

Le poids $\vec{\mathrm P} = m \vec g$ est la seule force qui s'exerce sur ce système : la deuxième loi de Newton permet d'écrire $\displaystyle \sum \overrightarrow{\rm F_{ext}} = \vec{\rm P} = m\overrightarrow{a_{\rm G}}$ soit  $m\vec g = m\overrightarrow{a_{\rm G}}$ et enfin $\overrightarrow{a_{\rm G}} = \vec g$.

Le vecteur accélération du centre d'inertie d'un solide lors d'une chute libre est égal au vecteur champ de pesanteur : la valeur de l'accélération ne dépend pas de la masse du solide.

Dans le référentiel terrestre, on choisit un repère d'espace orthonormal $(\mathrm O~; \vec i, \vec j, \vec k)$ tel que l'axe vertical $(\mathrm O~; \vec k)$ est dirigé vers le haut.

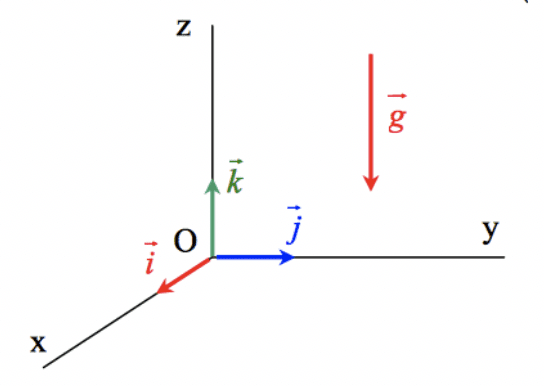
La relation vectorielle $\overrightarrow{a_{\rm G}} = \vec g$ permet d'écrire les coordonnées du vecteur accélération du centre d'inertie du solide puisqu'on connaît celles de $\vec g$.

\[\overrightarrow{a_{\rm G}}(t) = \left\{ \begin{array}{lll}
a_x(t) = 0\\
a_y(t) = 0\\
a_z(t) = -g\\
\end{array}\right.\]