Diagramme d’état d’un corps pur :
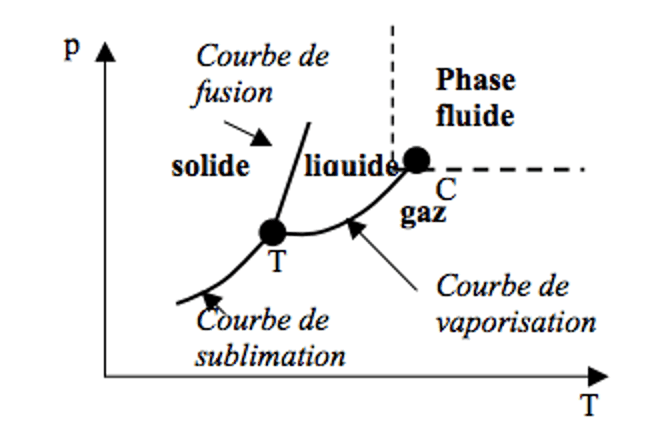
Les trois courbes se rejoignent au point triple $\rm (T)$.
La courbe de vaporisation est limitée par le point critique $\rm C$ au-delà duquel la différence entre liquide et gaz n’est plus possible, on parle alors de fluide super-critique.
On définit l’énergie massique de changement d’état $\rm L$ ou énergie latente de changement d’état en $\rm J.kg^{-1}$. L’énergie $\rm Q$ transférée lors du changement d’état d’une masse d’une espèce est $\rm Q = m \times L$ avec $\rm Q$ en $\rm J$ et $\rm m$ en $\rm kg$.
Si $\rm Q > 0$ alors transformation endothermique. Pour déterminer l’énergie massique de changement d’état, on utilise un calorimètre. Lors d’une fusion, une vaporisation ou une sublimation, l’énergie de l’espèce augmente et celle du milieu extérieur diminue (il se refroidit) : le transformation est endothermique. Lors d’une solidification, une liquéfaction ou une condensation, l’énergie de l’espèce diminue et celle du milieu extérieur augmente (il se réchauffe) : la transformation est exothermique.
Enthalpie de changement d’état
L'enthalpie de changement d'état d'un corps pur est par définition la variation d'enthalpie qui accompagne un changement d'état du corps rapportée à la quantité de matière mise en jeu lors de cette transformation. Par exemple pour le passage de l'état liquide à l'état de vapeur, on parle d'enthalpie de vaporisation.
L'enthalpie de changement d'état, notée $\rm \Delta_{1\rightarrow 2}H$, est exprimée en $\rm J/mol$ dans le Système international d'unités mais elle peut aussi être rapportée à l'unité de masse mise en jeu lors de la transformation : elle est alors exprimée en $\rm J/kg$ et est dite massique.
Enthalpie standard de formation :
On appelle enthalpie standard de formation d’une substance, notée $\Delta_f \rm H°$, l’enthalpie standard de la réaction de formation d’une mole de cette substance, $\Delta_r \rm H°$ , dans son état standard, à partir des corps purs simples pris dans leur état standard de référence.
$\scriptstyle\Delta_f \rm H°\text{(corps simple dans son état standard de référence)} = 0$
Enthalpie standard de réaction et loi de Hess :
L'enthalpie standard de réaction se calcul à partir des enthalpies standard de formation selon :
$\Delta_r \rm H°(T)$ $= \displaystyle \sum_i v_i \Delta_f \rm H°_{\mathcal i}(T)$ avec $\nu < 0$ pour les réactifs et $\nu > 0$ pour les produits.
Capacité thermique
$\rm \Delta H = C_p(T_2-T_1) = C_p \Delta T$ avec $\rm C_p$ La capacité thermique à volume constant en $\rm J.K^{-1}$.
On peut aussi définir :
- La capacité thermique molaire à pression constante $\rm C_{p_m} = \dfrac{C_p}{n}$ en $\rm J.K^{-1}.mol^{-1}$ où $n$ est le nombre de moles de corps purs contenues dans le système.
- La capacité thermique massique à pression constant $\rm C_p = \dfrac{C_p}{m_{syst} = \mathcal nm$ d'où $\rm C_v = \dfrac{C_{v_m}}{M}$ avec $\rm M$ masse molaire du corps pur considéré.
Donc $\boxed{\scriptstyle\rm\Delta H = C_p (T_2-T_1) = C_p\Delta T = m_{syst}C_p\Delta T}$
