Une lentille est un objet transparent capable de réfracter la lumière. Une lentille mince (diamètre très grand par rapport à son épaisseur) convergente a des bords plus fins que son centre.
Elle est schématisée par : 
$\rm F$ est le foyer objet, $\rm F’$ est le foyer image.
$\rm F$ et $\rm F’$ sont symétriques par rapport à $\rm O$.
La distance $\rm OF’$ est appelée distance focale.
Une lentille convergente a pour effet :
Construction graphique de l’image d’un objet :
Tout rayon passant par le centre $\rm O$ d'une lentille mince convergente ne subit aucune dérivation. Ce point $\rm O$ est appelé centre optique de la lentille.
Tout rayon parallèle à l'axe optique principal traverse la lentille convergente et passe par un point appelé foyer image $\rm F'$ de la lentille.
Il existe un point $\rm F$ sur l'axe principal tel que tout rayon passant par $\rm F$ et traversant la lentille convergente sort parallèlement à l'axe optique. On l'appelle foyer objet de la lentille.
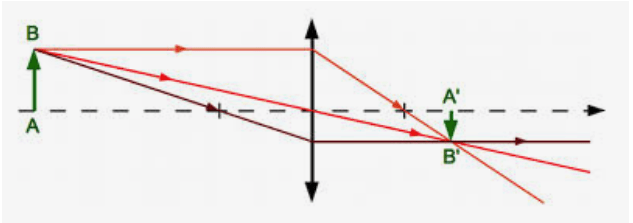
On définit le grandissement (sans unité) pour caractériser la taille de l’image d’un objet par une lentille par $\displaystyle \rm \gamma = \frac{A'B'}{AB}$ avec $\rm A’B’$ taille de l’image en $\rm m$ et $\rm AB$ taille de l’objet en $\rm m$. Si $\gamma > 1$ alors l’image est plus grande que l’objet.
Tout rayon parallèle à l'axe optique principal traverse la lentille convergente et passe par un point appelé foyer image $\rm F'$ de la lentille.
Pour un faisceau parallèle, tous les rayons émergeant de la lentille convergent en ce point.
Il existe un point $\rm F$ sur l'axe principal tel que tout rayon passant par $\rm F$ et traversant la lentille convergente sort parallèlement à l'axe optique. On l'appelle foyer objet de la lentille.
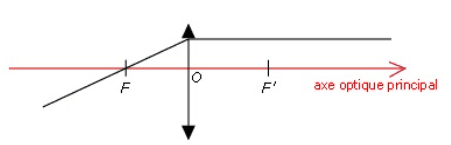
Une lentille convergente peut être utilisée indifféremment dans les deux sens car les distances $\rm OF$ et $\rm OF'$ sont égales.
La distance focale $\rm f'$ en mètre est la valeur algébrique de la distance du centre optique à un foyer $\rm F$ ou $\rm F'$ :
$\rm f' = \overline{FO} = \overline{OF'}$
La vergence d'une lentille est la grandeur définie par :
$\displaystyle \rm C = \frac{1}{f'}$
L'unité du système international est le $\rm m^{-1}$ mais l'unité usuelle est la dioptrie $(\sigma)$.
Pour une lentille convergente, $\rm f'$ et $\rm C$ sont des grandeurs positives.
L'axe optique principal est orienté dans le sens de propagation de la lumière (en général de la gauche vers la droite).
La position de l'objet sur l'axe optique principal est notée $\rm A$ et celle de l'image, $\rm A'$. Ces deux places sont déterminées respectivement par les valeurs algébriques $\rm \overline{OA}$ et $\rm \overline{OA}$.
L'objet se trouvant avant le centre optique $\rm O$, $\rm \overline{OA}$ est négatif. Au contraire, l'image se situant après $\rm O$, $\rm \overline{OA'}$ est positif.
La formule de conjugaison de Descartes permet de déterminer la distance $\rm \overline{OA}$ qui sépare l'image de l'objet du centre optique $\rm O$ :
$\displaystyle \rm \frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}}$ $\displaystyle \rm = \frac{1}{\overline{OF'}}$ avec les distances en mètres.
Le grandissement $\gamma$ est le rapport des tailles de l'objet $\rm AB$ et de son image $\rm A'B'$ :
$\displaystyle\rm \gamma = \frac{\overline{OA'}}{\overline{OA}}$ $\displaystyle \rm = \frac{\overline{A'B'}}{\overline{AB}}$ avec $\rm AB$ ET $\rm A'B'$ en mètres et $\gamma$ sans unité.
Si $\displaystyle\rm \frac{\overline{OA'}}{\overline{OA}}$ est positif, alors l'image est droite (c'est-à-dire dans le même sens que l'objet).
Si $\displaystyle \rm \frac{\overline{OA'}}{\overline{OA}}$ est négatif, alors l'image est inversée par rapport à l'objet.
