Mouvement plan de chute libre
📝 Mini-cours GRATUIT
🍀 Fiches de révision PREMIUM

Les propriétés des matériaux et l'organisation de la matière

Les réactions d'oxydoréduction

Énergie transportée par la lumière
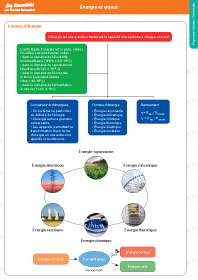
Énergie et enjeux
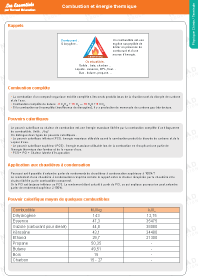
Combustion et énergie thermique

Énergie mécanique

Énergie chimique

Travail d'une force

Les réactions acido-basiques
🎲 Quiz GRATUIT
📄 Annale PREMIUM

Annales corrigées de maths – Métropole 2022



