Mouvements

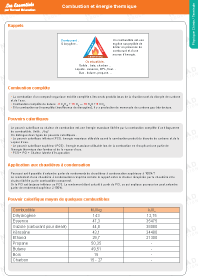
Le vecteur accélération

Le vecteur-accelération $\vec a (t)$caractérise la variation du vecteur-vitesse en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.

Le vecteur-accélération au point $\mathrm M_i$ s'écrit donc :

$\boxed{\overrightarrow{a(t)} = \frac{\mathrm d\vec v}{\mathrm dt} = \frac{\rm d^2\overrightarrow{OM}}{\mathrm dt^2}} \left\{\begin{array}{ll}t \text{ en s}\\ v \text{ en } \rm m.s^{1}\\ a \text{ en } \rm m.s^{-1}\end{array}\right.$

$\vec a(t) = a_x(t) \vec i + a_y (t) \vec j + a_z(t)\vec k$ avec $\vec a \left|\begin{array}{lll}a_x = \dfrac{\mathrm dv_x}{\mathrm dt} = \dfrac{\mathrm d^2x}{\mathrm dt^2}\\a_y = \dfrac{\mathrm dv_y}{\mathrm dt} = \dfrac{\mathrm d^2y}{\mathrm dt^2}\\a_z = \dfrac{\mathrm dv_z}{\mathrm dt} = \dfrac{\mathrm d^2z}{\mathrm dt^2}\end{array}\right.$

Les caractéristiques du vecteur-accélération sont les suivantes :

$\vec a(t)\left\{\begin{array}{lll}\scriptstyle \text{direction : celle du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{sens : celui du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{valeur (norme) : } a = \frac{\Delta v}{\Delta t} = \|\vec a\| = \sqrt{a_a^2+a_y^2+a_z^2}\end{array}\right.$

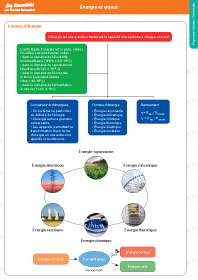
Des exemples de mouvements

Mouvements rectilignes