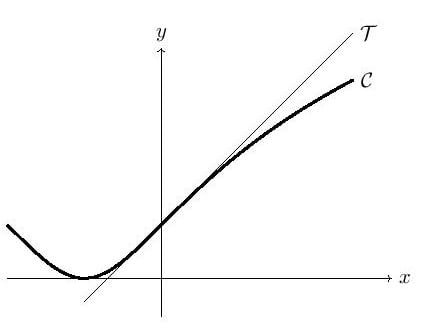
Les termes de degré $\leq 1$ du développement limité d'une fonction permettent d'obtenir l'équation de la tangente.
La position relative de la tangente par rapport à la courbe repose sur le théorème suivant :
Théorème :
Deux fonctions équivalentes au voisinage d'un point sont de même signe au voisinage de ce point.
Méthode :
Soit une fonction $f$ dérivable au voisinage de $x_0$.
- Pour calculer l'équation de la tangente $(\mathrm T)$ au point d'abscisse $x_0$ à la courbe $(\mathrm C): y =f(x)$, on effectue le $\mathrm{DL}_1(x_0)$ de $f$. $f(x) \stackrel{x \rightarrow 0}{=} a_0+a_1x + \mathrm o(x).$
L'équation de $(\mathrm T)$ est alors $y=a_0+a_1x$.
- Pour étudier la position relative de $(\mathrm C)$ par rapport à $(\mathrm T)$, on effectue un $\mathrm{DL}_n(x_0)$ de $f$ avec $n$ au moins égal à $2$. Le signe du premier terme non nul du développement limité de $\delta(x) = f(x) -(a_0+a_1x)$ permet de déterminer la position de $(\mathrm C)$ par rapport à $(\mathrm T)$.
Exemple :
Calculons l'équation de la tangente $(\mathrm T)$ à la courbe $(\mathrm C)$: $y= \ln(x^2+2x+2)$ au point d'abscisse $0$, puis déterminons la position relative de $(\mathrm T)$ par rapport à $(\mathrm C)$.
Notons $f$ la fonction définie par $f(x) = \ln(x^2+2x+2)$. Un développement limité de $f$ à l'ordre $1$ : $f(x) \stackrel{x \rightarrow 0}{=} a_0+a_1x+\mathrm o(x)$ est suffisant pour obtenir l'équation de la tangente.
Pour étudier la position relative de $(\mathrm T)$ par rapport à $(\mathrm C)$, on étudie localement (c'est-à-dire au voisinage de $0$ ici) le signe de la fonction $\delta(x) = f(x) - (a_0+a_1x).$
Or on a $\delta(x) \stackrel{x \rightarrow 0}{=}\mathrm o(x)$. L'ordre $1$ ne suffit pas pour déterminer un équivalent de $\delta(x)$ et ainsi son signe. On utilise en effet le fait que deux fonctions équivalentes en un point ont le même signe au voisinage de ce point.
Il faut donc effectuer un développement limité à l'ordre $2$. On se ramène à la fonction de référence $\ln(1+u)$ en écrivant :
$\displaystyle f(x)=\ln\left(2\left(1+x+\frac{1}{2}x^2\right)\right)$ $\displaystyle = \ln(2)+\ln\left(1+x+\frac{1}{2}x^2\right)$.
$\displaystyle{\ln\left(1+x+\frac{1}{2}x^2\right)=\ln(1+u)}$ avec $\displaystyle{u=x+\frac{x^2}{2} \rightarrow 0}$. (Notons que le développement limité de la fonction $\displaystyle{x \mapsto x+\frac{x^2}{2}}$ est elle-même puisque c'est une fonction polynomiale).
On sait que $\displaystyle{\ln(1+u)\stackrel{u \rightarrow 0}{=}u-\frac{u^2}{2} + \mathrm o(u^2)}$.
Le tableau de composition s'écrit alors :
$$\begin{array}{|c|l|}
\hline
\mathrm P(x) & x + \frac{x^2}{2} \\
\hline
\mathrm P^2(x) & x^2 \\
\hline
\mathrm P(x)-\frac{P^2(x)}{2} & x\\
\hline
\end{array}$$
On a donc $f(x) \stackrel{x \rightarrow 0}{=} \ln(2) +x + \mathrm o(x^2)$. On en déduit que l'équation de la tangente est $y=\ln(2)+x.$
Le $\mathrm{DL}_2(0)$ de $\delta$ est d'après le calcul précédent :
$\delta(x) = f(x)-\left(\ln(2)+x\right)\stackrel{x \rightarrow 0}{=} 0 + \mathrm o(x^2).$
Il s'avère que l'ordre $2$ n'est pas suffisamment pour pouvoir obtenir un équivalent de $\delta$ au voisinage de $0$. On doit aller à l'ordre $3$.
On sait (ou on retrouve) que $\displaystyle{\ln(1+u) \stackrel{u \rightarrow 0}{=} u - \frac{u^2}{2} + \frac{u^3}{3} + o(u^3)}$.
Le tableau de composition s'écrit :
$$\begin{array}{|c|c|} \hline \mathrm P(x) & x + \frac{x^2}{2} \\
\hline
\mathrm P^2(x) & x^2 + x^3\\ \hline
\mathrm P^3(x) & x^3 \\
\hline
\mathrm P(x)-\frac{P^2(x)}{2} + \frac{\mathrm P^3(x)}{3!} & x+\left(-\frac{1}{2}+\frac{1}{6}\right)x^3\\
\hline
\end{array}$$
On a donc $\displaystyle{f(x) \stackrel{x \rightarrow 0}{=} \ln(2) +x -\frac{x^3}{6}+o(x^3)}$. On en déduit que
$\displaystyle \delta(x) = f(x)-\left(\ln(2)+x\right)\stackrel{x \rightarrow 0}{=}$ $\displaystyle -\frac{x^3}{6} + o(x^3)$ donc $\displaystyle{\delta(x)\stackrel{x \rightarrow 0}{\sim} -\frac{x^3}{6}}$.
Le signe de $\delta(x)$ est donc celui de $-x^3$ au voisinage de $0$. On en déduit que :
- Au voisinage de $0^+$, la courbe $(\mathrm C)$ est en-dessous de la tangente $(\mathrm T)$
- Au voisinage de $0^-$, la courbe $(\mathrm C)$ est au-dessus de la tangente $(\mathrm T)$.