Le référentiel est un endroit de référence par rapport auquel on étudie le mouvement d’un mobile.
A chaque référentiel est associé :
- Un repère d’espace pour quantifier la position ;
- Un repère de temps (une horloge) pour associer une date à chaque position.
La position d'un mobile $\rm M$ dans un repère $(\mathrm O, \vec i, \vec j, \vec k)$ est donnée par son vecteur-position $\rm \overrightarrow{OM}$ :
\[\overrightarrow{\rm OM} (t) \left(\begin{array}{ccc}
x(t)\\
y(t)\\
z(t)\\
\end{array}\right) \Leftrightarrow \overrightarrow{\rm OM}(t) = x(t) \vec i + y(t) \vec j + z(t)\vec k\]
L'ensemble des points occupés successivement par le mobile $\rm M$ au cours du temps est appelé trajectoire.
Le vecteur vitesse :
Le vecteur-vitesse $\vec v(t)$ caractérise la variation du vecteur-position en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.
Le vecteur-vitesse instantanée au point $\rm M_i$ s'écrit donc :
\[\color{\black}{\boxed{\overrightarrow{v(t)} = \frac{d\overrightarrow{\rm OM}}{dt}} \left\{\begin{array}{lll}
t \text{ en s}\\
\text{OM en m}\\
v \text{ en m.s^{-1}}\\
\end{array}\right.}\]
$\vec v(t) = v_x(t)\vec i + v_y(t)\vec j + v_z(t)\vec k = \dot{x}\vec i + \dot{y}\vec j + \dot{z}\vec k$
Notation :
- $\displaystyle v_x(t) = \dot{x} = \frac{dx}{dt}$
- $\displaystyle v_y(t) = \dot{y} = \frac{dy}{dt}$
- $\displaystyle v_z(t) = \dot{z} = \frac{dz}{dt}$
Les caractéristiques du vecteur-vitesse sont les suivantes :
\[\overrightarrow{v(t)}\left\{\begin{array}{lll}
\text{direction : tangent à la trajectoire}\\
\text{sens : celui du mouvement}\\
\text{valeur (norme) : } \left\|\vec v\right\| = v = \sqrt{v_x^2 + v_y^2 + v_z^2}\\
\end{array}\right.\]
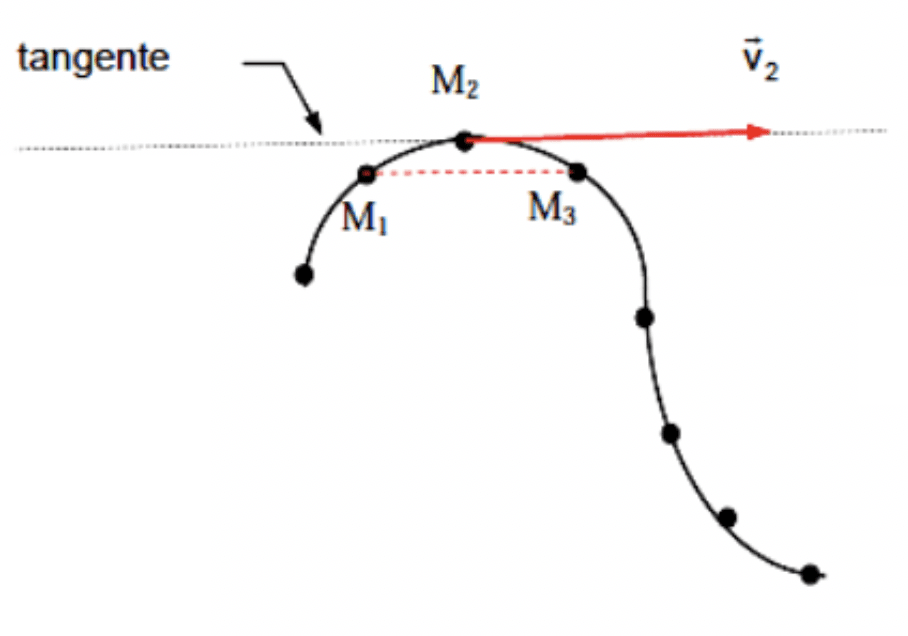
\[\color{black}{\boxed{\textbf{CONSTRUCTION D'UN VECTEUR VITESSE}}}\]
Le vecteur vitesse moyen $\rm \vec v(t_2)$ au point $\rm M_2$ à la date $\rm t_2$ s'écrit : $\color{black}{\boxed{\rm \vec v (t_2) = \frac{\overrightarrow{M_1M_2}}{T_1-t_2}}}$.
Le vecteur vitesse $\bf \vec v (t_2)$ possède :
- Une direction : la tangente à la trajectoire au point $\rm M_2$, parallèle à la droite $\rm M_1M_3$.
- Un sens : celui du mouvement.
- Une valeur : $\rm \displaystyle v_2 = \frac{M_1M2}{t_1 -t_2} = \frac{M_1M_3}{2\tau} = v_2$ s'exprime en $\rm m.s^{-1}$.
($\tau$ : intervalle de temps constant entre deux points consécutifs). - Une longueur : donnée par une échelle des vitesses (exemple = $\rm 1~cm \leftrightarrow 0,1~m.s^{-1}$).
Le vecteur variation de vitesse :
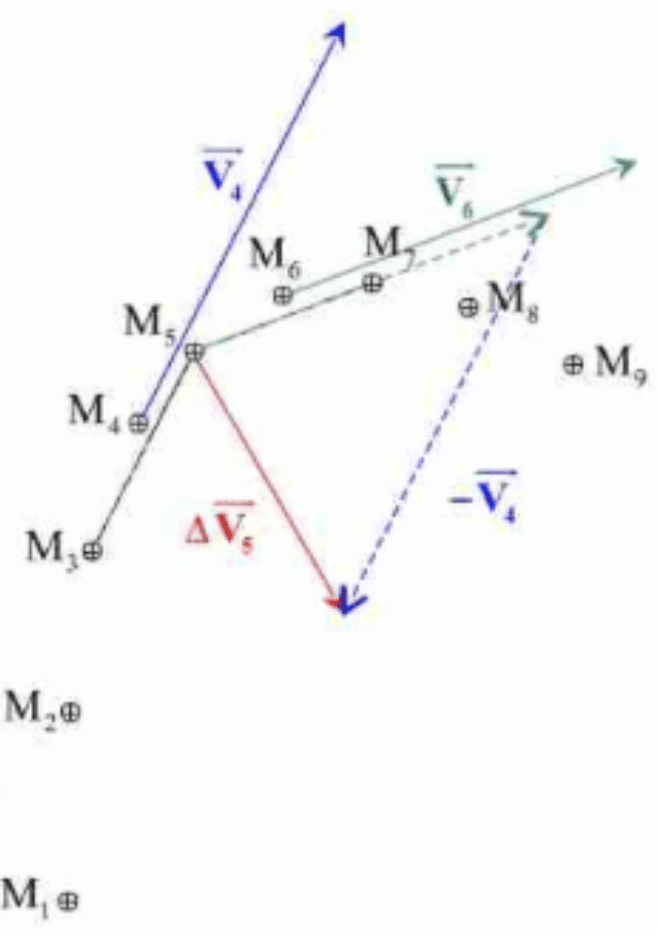
Comment construire le vecteur $\bf \overrightarrow{\Delta V_5} = \overrightarrow{V_6} - \overrightarrow{V_4}$ ?
- Tracer les vecteurs vitesses $\rm \overrightarrow{V_4}$ et $\rm\overrightarrow{V_6}$.
- Au point $\rm M_5$, reconstruire le vecteur $\rm \overrightarrow{V_6}$.
- Construire le vecteur $\rm - \overrightarrow{V_4}$ depuis l'extrémité du vecteur $\rm\overrightarrow{V_6}$ reconstruit juste avant.
- Le vecteur $\rm \overrightarrow{\Delta V_5}$ est le vecteur qui joint l'origine de $\rm \overrightarrow{V_6}$, point $\rm M_5$, à l'extrémétité de $-\rm\overrightarrow{V_4}$.
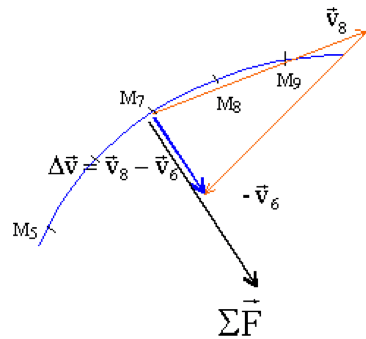
La somme des forces appliquées au système :
\[\displaystyle {\color{cyan}{\boxed{\color{black}{\rm \sum\vec F_{ext}}} \color{black}{\rm = m \times \frac{\color{cyan}{\boxed{\color{black}{\Delta \vec v}}}}{\Delta t}}}}\]
Le rôle de la masse du système :
Plus la masse du système est grande, plus la variation du vecteur vitesse est faible pour une même somme des forces appliquées.
Le vecteur-accélération $\vec a(t)$ caractérise la variation du vecteur-vitesse en fonction du temps comme la dérivée par rapport au temps du vecteur-vitesse.
Le vecteur-accélération au point $\rm M_i$ s'écrit donc :
\[\color{black}{\boxed{\displaystyle \vec a(t) = \frac{d\vec v}{dt} = \frac{d^2\rm \overrightarrow{OM}}{dt^2}}}\left\{\begin{array}{lll} t \text{ en s}\\
v \text{ en }\rm m.s^{-1}\\
a \text{ en } \rm m.s^{-2}\\
\end{array}\right.\]
$\vec a(t) = a_x(t) \vec i + a_y(t) \vec j + a_z (t) \vec k$ $= \dot{v}_x \vec i + \dot{v}_y \vec j + \dot{v}_z \vec k$ $= \ddot{x} \vec i + \ddot{y} \vec j + \ddot{z}\vec k$
Notation : $\displaystyle a_x(t) = \frac{dv_x}{dt} = \frac{d^2x}{dt^2} = \ddot{x}$
De même pour $a_y$ et $a_z$.
Les caractéristiques du vecteur-accélération sont les suivantes :
\[\scriptstyle\overrightarrow{a(t)}\left\{\begin{array}{lll} \text{direction : celle du vecteur } \overrightarrow{\Delta v}(t)\\
\text{sens : celui du vecteur } \overrightarrow{\Delta v}(t)\\
\text{valeur (norme) : } a = \frac{\Delta v}{\Delta t} = \left\|\vec a\right\| = \sqrt{a_x^2 + a_y^2 + a_z^2}\\
\end{array}\right.\]
